Cross Entropy
Entropy
Entropy of a random variable X is the level of uncertainty inherent in the variables possible outcome.
Cross-Entropy loss is an important cost function. It is used to optimize classification models. The understanding of Cross-Entropy is pegged on understanding of Softmax activation function.
Consider a 4-class classification task where an image is classified as either a dog, cat, horse, or cheetah.
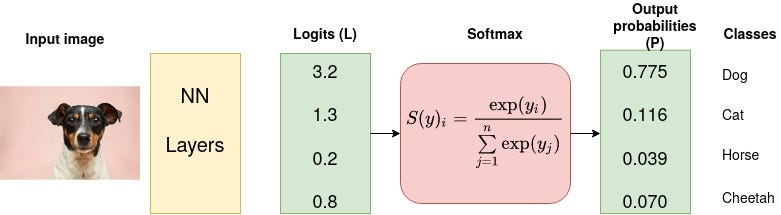
In the above Figure, Softmax converts logits into probabilities. The purpose of the Cross-Entropy is to take the output probabilities (P) and measure the distance from the truth values (as shown in Figure below).
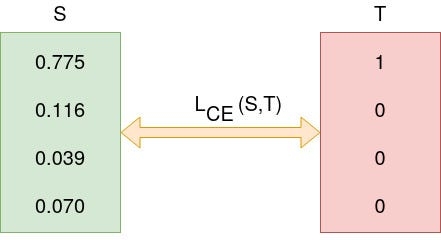
For the example above the desired output is [1,0,0,0] for the class dog but the model outputs [0.775, 0.116, 0.039, 0.070] .
Cross-Entropy Loss Function
Also called logarithmic loss, log loss or logistic loss. Each predicted class probability is compared to the actual class desired output 0 or 1 and a score/loss is calculated that penalizes the probability based on how far it is form the actual expected value. The penalty is logarithmic in nature yielding a large score for large differences close to 1 and small score for small differences tending to 0. Cross-entropy is defined as,
Categorial Cross-Entropy Loss
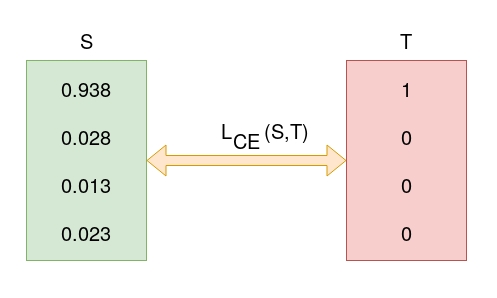
Assume that after some iterations of model training the model outputs the following vector of logits
Binary Cross-Entropy Loss
If there are just two class labels, the probability is modeled as the Bernoulli distribution for the positive class label. This means that the probability for class 1 is predicted by the model directly, and the probability for class 0 is given as one minus the predicted probability, for example,
Last updated
Was this helpful?